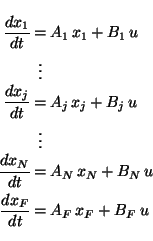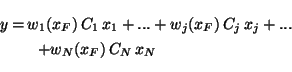

Next: CSTR Case Study
Up: Multiple Model Approach for
Previous: Local Modeling
In process systems where a linear model or controller proves insufficient, it
is desirable to have a simple representation that can model or control the nonlinear
system. This leads one to consider a multiple model approach. There are many
possible routes to take depending upon how much is known about the system.
- For this work, it is assumed that a first-principles model of the system under
consideration is not known, although a first-principles model is used for simulation
purposes.
- It is also assumed that the system does not exhibit output multiplicity. This
implies that there could be input multiplicities in the process, resulting in
a process optima with zero-gain.
- One final assumption is that local models may already be available for some
operating conditions, while new models can be developed at other operating points.
To best piece together multiple local models, one must devise a method for partitioning
the operating space for the system. For input multiplicity systems, it makes
sense to partition the space using the system's input values. Operating points
for the local models are chosen with regard to what existing models may be available,
the known process characteristics (such as process optima), and the desired
system operating range. In the next step for developing a multiple model system,
one must assume a method for weighting the independent local models. In order
to adequately capture steady-state values, a linear interpolation scheme is
used in this work. This means that the model weights are based on the nearest
two local models in the SISO case. When operating exactly at the point where
the model i was devised, the weight for model i should be equal
to 1. When operating halfway between two models each model should be weighed
equally, resulting in weights of 0.50. This model weighting scheme removes
the problems often associated with the normalization of overlapping basis functions
as presented in [Murray-Smith and Johansen(1997)]. The tail of a Gaussian model weight can extend
well into another model regime, causing a model to become active in the wrong
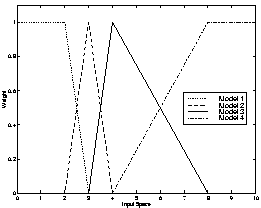
region. Typical model weights for the presented work are shown in Figure 1.
In this figure, the models would be established at the operating points 2,
3, 4 and 8 in the input space of the system. This type of weighting has also
been extended to a 2x2 MIMO case.
Figure 1:
Model Weighting Function
|
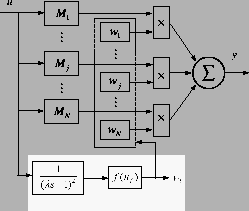
Using the process inputs to select the correct operating point works well for
steady-state analysis. When using this method of model switching, changes in
the process inputs will cause the process to jump from one model directly to
another. In order to allow for mixing of heterogeneous models, all local models
are given absolute process inputs and produce absolute process outputs. As
the process input changes from one value to another, the actual system does
not respond immediately. This means that the actual state of the process is
not moving instantaneously. To cope with this reality, the operating point
for model switching is based on a filtered value of the system inputs. The
filter is chosen with a time constant typical of the system. A second order
filter with unity gain is used in this work. This creates a realistically smooth
response that is continuously differentiable. See Figure 2
for a schematic. If one considers a linear state-space realization for each
model
Mj([Aj,Bj,Cj]), then the corresponding state-space
composite model is given by:
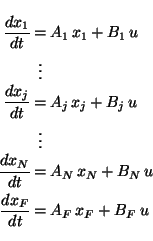
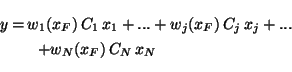
where xF corresponds to the states of the filter realization.
Note that this model is a Wiener structure, and it is piecewise bilinear. Consequently,
the rich literature on Wiener and bilinear systems is relevant to this approach.
Figure 2:
Model Weighting Schematic
|
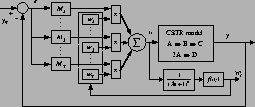
For control purposes, some work has to be done to make use of the model switching
techniques. First, a controller must be devised for each local model. For
this study, PI controllers were used for all local model controllers. These
were tuned using IMC tuning rules and typical process reaction curve parameters.
Use of IMC-PI form allows for a single tuning parameter for all controllers.
The total system error is given to each controller. The output of each controller
is multiplied by the current weights for each model. The total of all the weighted
controller outputs is taken as the actual process input. See Figure 3.
Figure 3:
Closed-loop Schematic
|


Next: CSTR Case Study
Up: Multiple Model Approach for
Previous: Local Modeling
Edward Price Gatzke
1999-07-12